2021年6月4日最終更新

どうも!
FP試験でも問われるお金にまつわる6つの係数を紹介していこう。
いつまでにお金を貯めようかとか、ローンがいくらまで組めるかなんてことがこの係数でわかる!
お金にまつわる6つの係数
お金にまつわる6つの係数がある。
あなたが100万円を運用して、配当や利息を複利でもらい続けたら10年後にいくらになるのか。
あなたが住宅ローンを組むときに毎月返済出来る額はいくらだろうか。
老後、手元にある1,000万円を30年間運用しながら取り崩して行ったときに毎月いくら使えるだろうか。
などなどを知ることが出来る「ライフプラン」を作成し将来設計をするのに役立ちます。
excelや表計算ソフトですぐに計算出来るが、どんな係数を利用しているのかを知っておいて損はない。
では、早速見てみよう!
6つの係数
6つの稀有数とは、終価係数・現価係数・年金終価係数・減債基金係数・年金現価係数・資本回収係数である。
簡単に説明すると、
- 終価係数
現在の金額を複利運用した場合の将来の金額 - 現価係数
将来の目標金額を得るために現在必要な金額 - 年金終価係数
毎年一定金額を積み立てた時の積立額 - 減債基金係数
将来の目標金額を得るために毎年の積立額 - 年金現価係数
将来一定期間にわたり一定額を受け取るための現在必要な金額 - 資本回収係数
現在の金額を一定期間で取り崩して行く場合の毎年の取り崩し金額
である。
似たような言葉が並びややこしいので、一つ一つ使う場面を説明していこう。
年金終価係数
年金終価係数(ねんきんしゅうかけいすう)は、一定の期間、一定の金額を毎年同額で積み立てながら、一定の利率で複利運用した場合、将来いくらになるかを計算するための係数である。
現在手元に大きな資産がない場合でも、月々積み立てることで目標金額を目指そうというものだ。
あなたが、100万円を毎年積み立てれば、10年後にいくらになるかが分かる。
ちなみに運用中は1年ごとの複利計算で行う。
公式は、やや難解になるので、年金終価係数表から数値を抜粋した。
年金終価係数 : 11.464
100万円 × 11.464 = 11,464,000円
そのままタンス預金にすると1,000万円だが、運用することで1,146万円にすることが出来る。
机上の空論だが、高額を長期にわたって積み立てるときは、投資においては負けにくいというドルコスト平均法を用いることが出来るので、投資は絶対嫌と言う方以外は是非試してほしい。
自分が貯めている金額より大きなものを購入するときに利用してほしい。
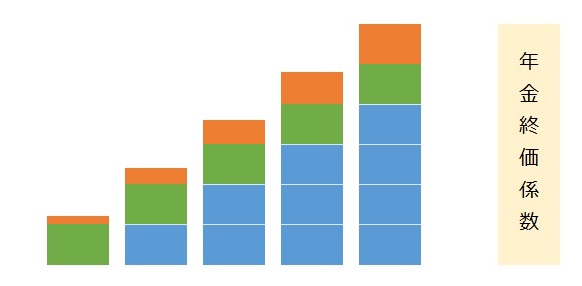
図の緑色と青色の部分が積み立てていく金額で、オレンジ色が複利運用による利息(配当等)である。そして、求める目標金額がオレンジ色+緑色+青色である。

簡単計算サイトを利用する
ネット上には、簡単に終価係数を使った計算が出来るサイトがある。
もし、あなたが将来必要な資金を入力すると今いくら運用すれば良いのかを即座に知ることができる。

注意点も!
現実に、年金終価係数を使って運用原資を計算してもその通りになることは少ない。
ただ、その近似値を出すことは出来る。
その理由は、第一に税金問題だ。
株やETF、投資信託の配当金には税金(約20%)がかかるからだ。税金を考慮して計算することは現価係数計算においては向かない。
次に、複利運用の難しさだ。配当金等を再投資しても投資口数による端数が必ず発生する。
100%効果的な複利運用は難しいだろう。
まとめ
年金終価係数は、将来設計をするためにも重要な指数だ。
ざっと計算するより、係数を利用して試算することが現実味があり、その現実味が将来設計を計画通りに進める原動力になるだろう。
ぜひ、あなたの将来設計に年金終価係数があることを覚えておいて欲しい。
今ある資産を何%の利回りで運用すれば目標金額がわかるので、現実的かどうかを判断する基準にもなる。
100万円を1,000万円に数年で増やすのはほぼ不可能だが、数十年スパンを考えるとそうでもないことが分かる。
複利利回りと年数を掛け算、乗算することでお金が増えていくということは非常に重要なことなので頭の片隅にでも置いておいてほしい。
子供の入学、車の新替え、老後の資産設計、住宅購入の頭金などの大きなライフイベントに備えるためにこの指数は利用できるだろう。

年金終価係数は、将来必要な資金を今から積み立てて運用したらいくら必要かを知ることが出来る係数である!
利回りが5%、6%と上がり、運用年数が長期間になるほど運用積立原資は少なくて済む!




コメント